Static Fields: Fall-2025
HW 01 Practice (SOLUTION): Due W1 D3: Math Bits
- Cube Charge
S1 5277S
-
Charge is distributed throughout the volume of a dielectric cube with
charge density \(\rho=\beta z^2\), where \(z\) is the height from the
bottom of the cube, and where each side of the cube has length \(L\).
What is the total charge inside the cube? Do this problem in two ways as both
a single integral and as a triple integral.
The charge density inside the cube is \(\rho=\beta z^2\).
The total charge is given by chopping the cube into infinitesimal cubical volumes \(d\tau=dx\, dy\, dz\). The charge on each piece is given by \(dq=\rho\, d\tau\) and the total charge is obtained by adding (integrating) the infinitesimal charges over the whole volume of the box.
\begin{align} Q_{\hbox{total}}&=\int_0^L\int_0^L\int_0^L \beta z^2\, dx\, dy\, dz\\ &=\beta\left(\int_0^L dx\right)\left(\int_0^L dy\right) \left(\int_0^L z^2\, dz\right)\\ &=\beta\, (L)^2(\frac{z^3}{3})\Big\vert_0^L\\ &=\beta\, \frac{L^5}{3} \end{align}
Rather than chopping the cube into infinitesimal cubical volumes, we could chop the cube into infinitesimally thin square slabs (parallel to the \(x-y\) plane) \(d\tau=L^2dz\). The charge on each slab is given by \(dq=\rho d\tau=\beta z^2L^2dz\). The total charge is obtained by adding (integrating) the infinitesimal charges over the whole volume of the box.
\begin{align} Q_{\hbox{total}}&=\int_0^L L^2 \beta z^2\, dz\\ &=\beta L^2 \left(\int_0^L z^2\, dz\right)\\ &=\beta\, (L)^2(\frac{z^3}{3})\Big\vert_0^L\\ &=\beta\, \frac{L^5}{3} \end{align}
Sense-making: The dimensions work out, as long as you remember that \(\beta\) has dimensions of C/m\(^5\). It's also valuable to note that the three integrals can be done independently of one another, which is not always true, but is often true (whenever the region of integration doesn't depend on one of the coordinates).
-
On a different cube: Charge is distributed on the surface of a cube with charge density \(\sigma=\alpha z\) where \(z\) is the height from the bottom of the cube, and where each side of the cube has length \(L\). What is the total charge on the cube? Don't forget about the top
and bottom of the cube.
The charge density on the bottom of the cube is \(\sigma=\alpha z\) where \(z=0\). Therefore, there is no charge on the bottom of the cube.
The charge density on the top of the cube is \(\sigma=\alpha z\) where \(z=L\). Since the charge density is constant on the top of the cube, we can simply multiply the charge density times the area. The contribution of the top of the cube to the total charge is therefore \begin{equation} Q_{\hbox{top}}=\alpha\, L \times L^2=\alpha\, L^3 \end{equation}
The charge density on the sides of the cube is not constant, therefore we must integrate. The contribution from each of the four sides is the same, so we will calculate the contribution from one side and multiply by four. \begin{align} Q_{\hbox{sides}}&=4\int_0^L\int_0^L \alpha z\, dx\, dz\\ &=4\alpha\left(\int_0^L dx\right)\left(\int_0^L z\, dz\right)\\ &=4\alpha\, (L)(\frac{L^2}{2})\\ &=2\alpha\, L^3 \end{align}
The total charge is therefore: \begin{equation} Q_{\hbox{total}}=\alpha\, L^3+2\alpha\, L^3=3\alpha\, L^3 \end{equation}
Sense-making: Well, our dimensions work out again (note that \(\alpha\) does not have the same dimensions as \(\beta\) above).
Notice again that in the second line, because the integrand depends on only one variable, the double integral breaks up into separate integrals over \(x\) and \(z\).
Another way to make sense of a problem like this one would be to think about how things would change if we started with different initial conditions. For example, how would the solution of this problem have been different if the charge density had been \(\sigma = \beta xyz\)?
-
Charge is distributed throughout the volume of a dielectric cube with
charge density \(\rho=\beta z^2\), where \(z\) is the height from the
bottom of the cube, and where each side of the cube has length \(L\).
What is the total charge inside the cube? Do this problem in two ways as both
a single integral and as a triple integral.
- Curvilinear coordinate drawings
S1 5277S
-
Using the conventions from class for cylindrical and spherical coordinates, draw each of the surfaces below by hand:
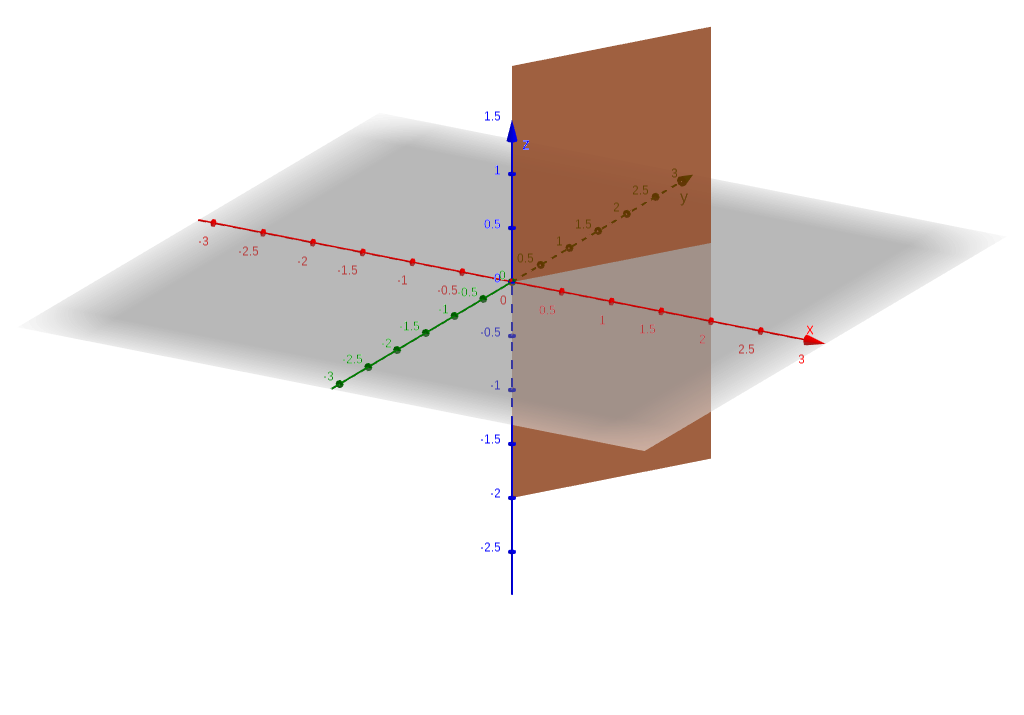
- \(\phi=\frac\pi3\)
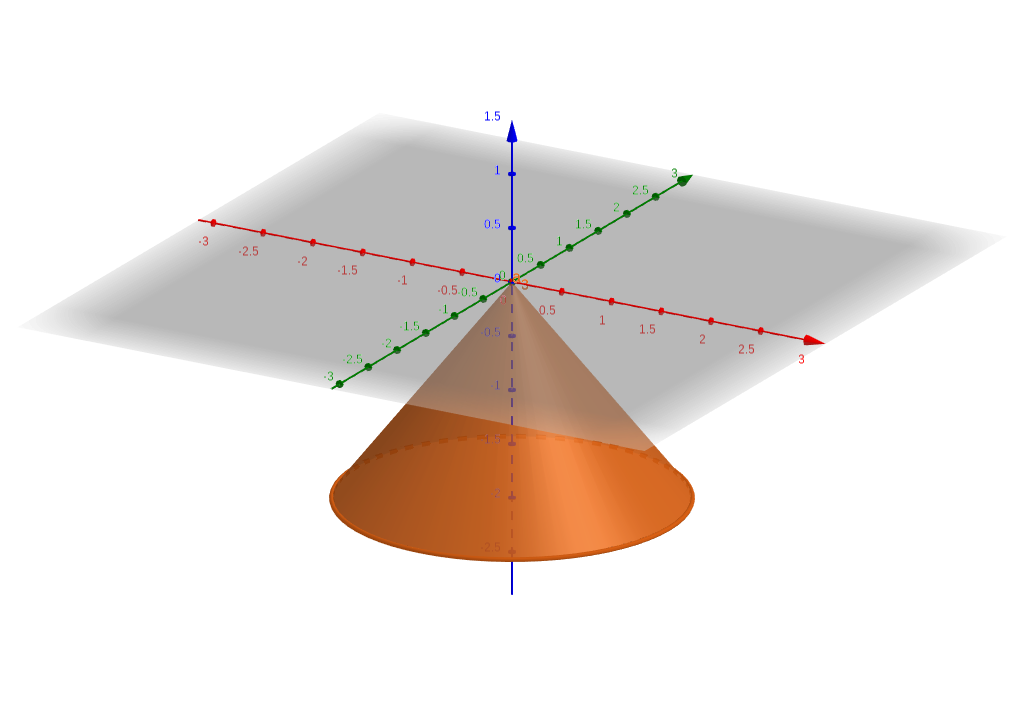
- \(\theta=\frac{3\pi}4\)
-
Using the conventions from class for cylindrical and spherical coordinates, draw each of the following vectors by hand at the indicated point.
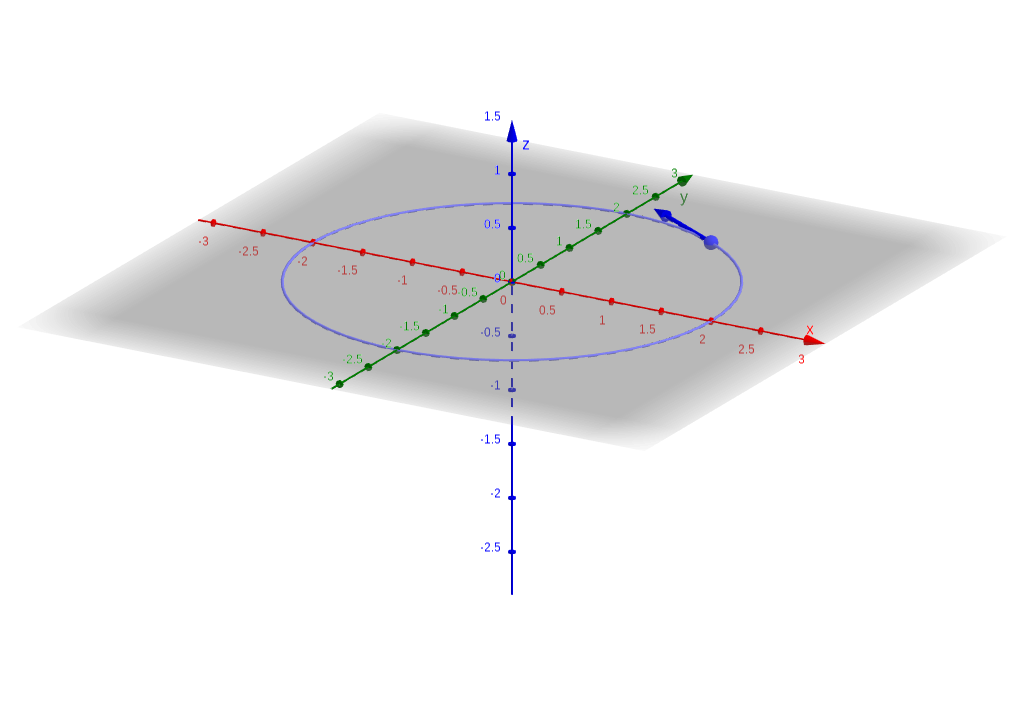
- \(\boldsymbol{\hat\phi}\) at the point where \(s=2\), \(\phi=\frac\pi3\), and \(z=0\).
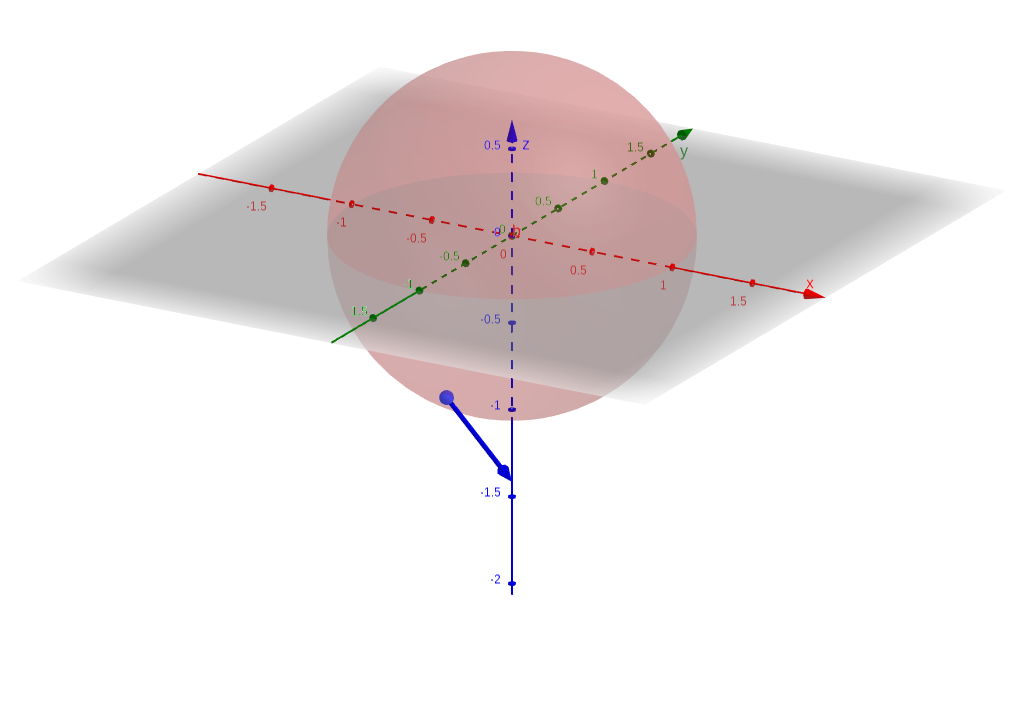
- \(\boldsymbol{\hat\theta}\) at the point where \(r=1\), \(\theta=\frac{3\pi}4\), and \(\phi=\frac\pi2\).
The figures below use the default orientation for GeoGebra, with the positive \(y\) axis pointing into the page.
-
Using the conventions from class for cylindrical and spherical coordinates, draw each of the surfaces below by hand:
- Exponential and Logarithm Identities S1 5277S Make sure that you have memorized the following identities and can use them in simple algebra problems: \begin{align*} e^{u+v}&=e^u \, e^v\\ \ln{uv}&=\ln{u}+\ln{v}\\ u^v&=e^{v\ln{u}} \end{align*}
- Derivative Rules
S1 5277S
Make sure that you have memorized or can quickly find the derivative of all of the common transcendental functions: powers, trigonometric functions (especially sine and cosine), exponential, logarithms. Make sure that you can use these rules, even when the argument has parameters in it, e.g. \(\sin{kx}\). Also, make sure you can use the chain rule.
If you don't have these memorized, at least have a place that you can quickly locate them online or in a textbook.
- Basic Calculus: Practice Exercises
S1 5277S
Determine the following derivatives and evaluate the following integrals, all by hand. You should also learn how to check these answers on Wolfram Alpha.
- \(\frac{d}{du}\left(u^2\sin u\right)\)
Use the product rule: \begin{align} \frac{d}{du}\left(u^2\sin u\right) &=\left(\frac{d}{du}u^2\right)\sin(u)+u^2\frac{d}{du}(\sin u)\\ &=2u\,\sin u+u^2\cos u \end{align}
- \(\frac{d}{dz}\left(\ln(z^2+1)\right)\)
Use the chain rule: Setting \(w=z^2+1\), \begin{align} \frac{d}{dz}\left(\ln(z^2+1)\right) &=\frac{d}{dz}(\ln w)\\ &=\frac{d}{dw}(\ln w)\frac{dw}{dz}\\ &=\left(\frac1w\right)(2z)\\ &=\frac{2z}{z^2+1} \end{align}
Use the "onion" rule: \begin{align} \frac{d}{dz}\left(\ln(z^2+1)\right) &=\frac{1}{z^2+1}\frac{d}{dz}(z^2+1)\\ &=\frac{2z}{z^2+1} \end{align}
- \(\displaystyle\int v\cos(v^2)\,dv\)
Use substitution! Set \(w=v^2\), \(dw=2v\,dv\), and thus \begin{align} \int v\cos(v^2)\,dv &=\frac12\int \cos(w)\,dw\\ &=\frac12\sin(w)+C\\ &=\frac12\sin(v^2)+C\\ \end{align}
- \(\displaystyle\int v\cos v\,dv\)
Use integration by parts! Setting \(p=v\) and \(dq=\cos v\,dv\), \(dp=dv\) and \(q=\sin v\), so \begin{align} \int v\cos v\,dv &=\int p\,dq = \left. pq\right\vert_{\rm{boundary}} - \int q\,dp\\ &= \left. v\sin v\right\vert_{\rm{boundary}}-\int \sin v\,dv\\ &= \left. v\sin v\right\vert_{\rm{boundary}} + \left. \cos v\right\vert_{\rm{boundary}} \end{align}
- \(\frac{d}{du}\left(u^2\sin u\right)\)