Static Fields: Fall-2025
HW 04 Practice: Due W2 D5
- Sensemaking from Graphs of Power Series II
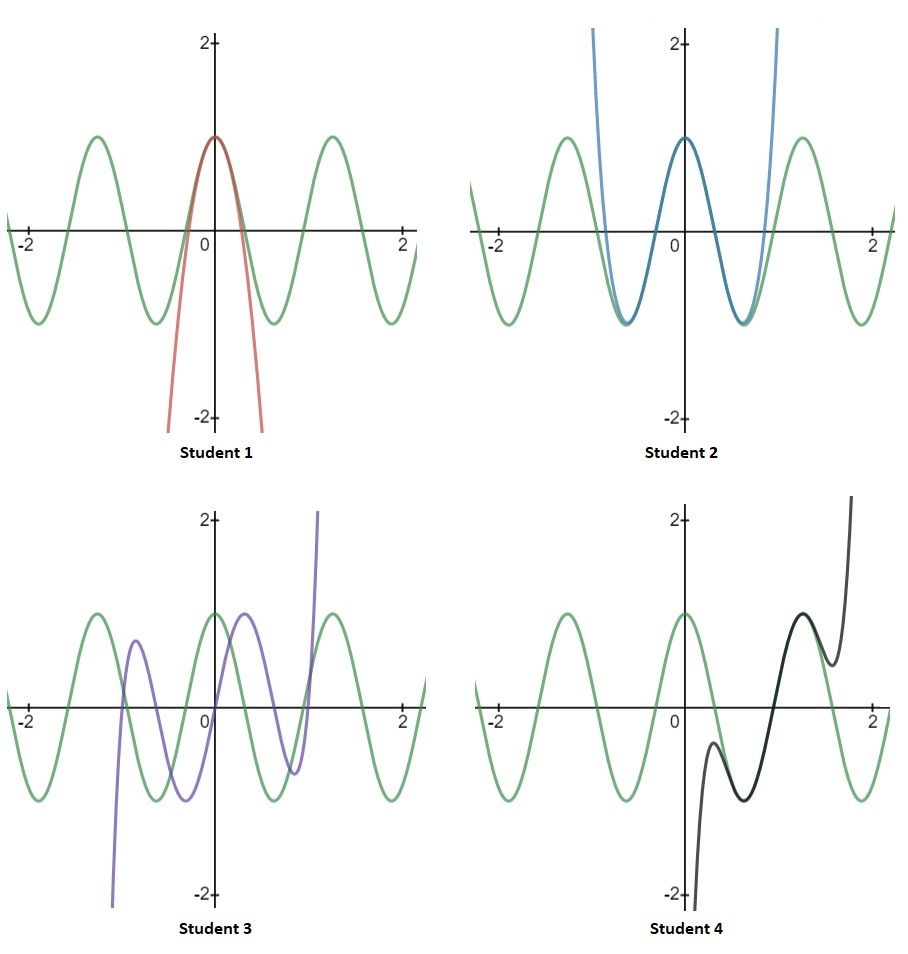
Four students attempted to find a Power Series approximation for \(\cos(5x)\) (graphed in green on all plots). In a few sentences, qualitatively describe what each student did and describe the range of values of \(x\) values for which their approximation is valid.
Of course, whether or not an “approximation is valid” depends a lot on how much accuracy you need in a given application.
Here, we will first mean that the qualitative features are correct, e.g. that the approximation is not increasing when the function is decreasing or the approximation is not concave up when the function is concave down. Next, we will mean that the approximation doesn't differ “too much” from the function. “Too much” is very much open to the interpretation of the person making the decision. (Don't worry - if I have a specific interpretation in mind, I will tell you. Especially on a quiz or exam!)
Some possible criteria are: "I can't tell the function on the graph from the approximation due to the thickness of the lines on the graph", "I need the function and the approximation to agree within 5%" (or whatever percentage you choose), or "My experimental data is valid to the third decimial place so the approximation should agree to that accuracy".
When you are asked a prompt like this, don't over think it. Make a professional choice about what you mean in this context and state what criterion you used. There is no wrong answer. Some examples of things you can say are given in the solutions.