Static Fields: Fall-2025
HW 07 Practice: Due W4 D3
- Flux through a Cylinder
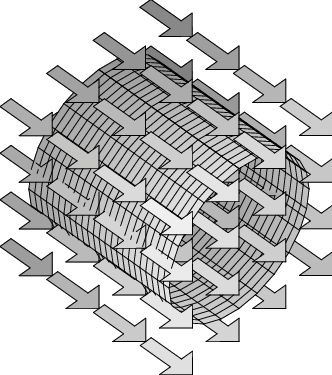
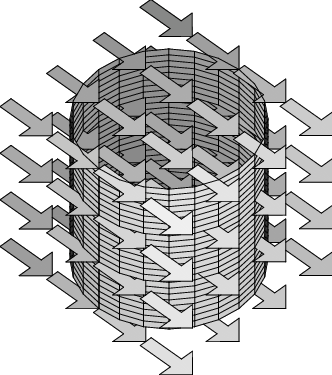
- What do you think will be the flux through the cylindrical surface that is placed as shown in the constant vector field in the first figure?
- What if the cylinder is placed upright, as shown in the second figure? Explain.
- Flux I Find the flux of \(\boldsymbol{\vec F} =x\,\boldsymbol{\hat x}+y\,\boldsymbol{\hat y} +z\,\boldsymbol{\hat z}\) out of a closed cylinder of radius 2 centered on the \(z\)-axis, with \(-3\le z\le3\).
- Flux II Find the flux of \(\boldsymbol{\vec F}=z^2\,\boldsymbol{\hat z}\) through the upper hemisphere of the sphere \(x^2+y^2+z^2=25\), oriented away from the origin.
- Flux III Let \(\boldsymbol{\vec H} = (e^{xy}+3z+5)\,\boldsymbol{\hat x} + (e^{xy}+5z+3)\,\boldsymbol{\hat y} + (3z+e^{xy})\,\boldsymbol{\hat z}\). Calculate the flux of \(\boldsymbol{\vec H}\) through the square of side \(2\) with one vertex at the origin, one edge along the positive \(y\)-axis, one edge in the \(xz\)-plane with \(x>0\), \(z>0\), and with normal \(\boldsymbol{\hat n}=\boldsymbol{\hat x}-\boldsymbol{\hat z}\).
- Flux through a Plane Find the upward pointing flux of the vector field \(\boldsymbol{\vec{H}}=2z\,\boldsymbol{\hat{x}} +\frac{1}{x^2+1}\boldsymbol{\hat{y}}+(3+2z)\boldsymbol{\hat{z}}\) through the rectangle \(R\) with one edge along the \(y\) axis and the other in the \(xz\)-plane along the line \(z=x\), with \(0\le y\le2\) and \(0\le x\le3\).
- Gauss's Law for a Rod inside a Cube Consider a thin charged rod of length \(L\) standing along the \(z\)-axis with the bottom end on the \(x,y\)-plane. The charge density \(\lambda_0\) is constant. Find the total flux of the electric field through a closed cubical surface with sides of length \(3L\) centered at the origin.
- Volume Charge Density
Consider the volume charge density: \begin{equation*} \rho (x,y,z)=c\,\delta (x-3) \end{equation*}
- Describe in words how this charge is distributed in space.
- What are the dimensions of the constant \(c\)?