Static Fields: Fall-2025
HW 10: Due W5 D5
- Ampere's Law for a Cylinder
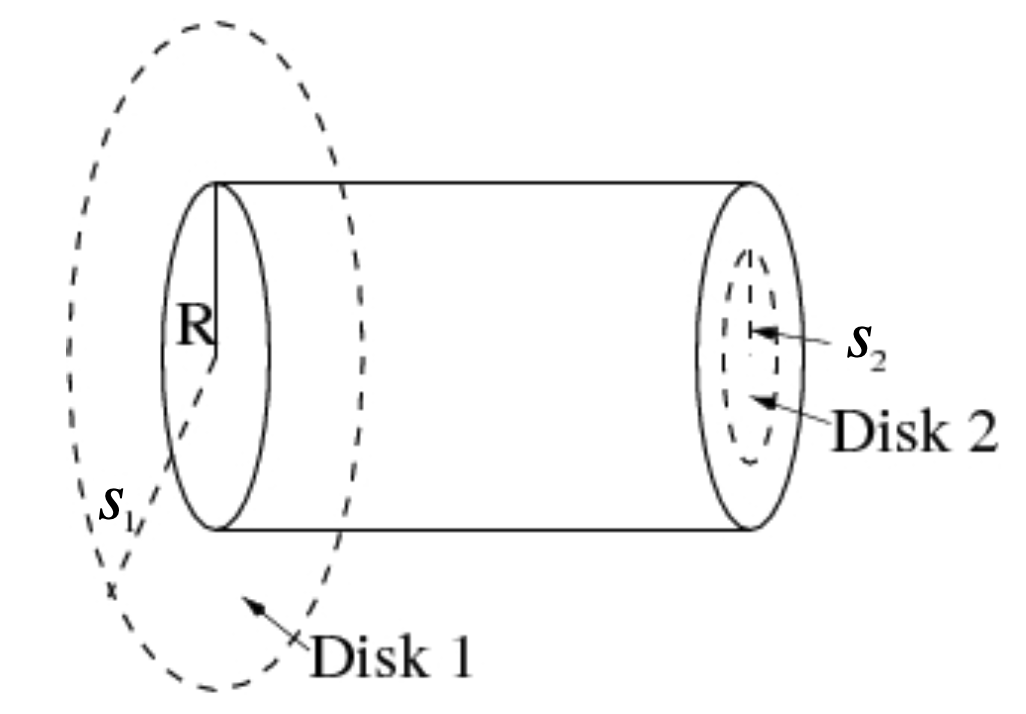
In this problem, you will be investigating a cylindrical wire of finite radius \(R\), carrying
a non-uniform current density \(J=\kappa s \;\hat{z}\), where \(\kappa\) is a
constant and \(s\) is the distance from the axis of the cylinder.
-
Find the total current flowing through the wire.
-
Find the current flowing through Disk 2, a central (circular
cross-section) portion of the wire out to a radius \(s_2<R\).
-
Use Ampere's law to find the magnetic field at a
distance \(s_1\) outside the wire.
-
Use Ampere's law to find the magnetic field at a
distance \(s_2\) inside the wire.
-
Find the total current flowing through the wire.
- Magnetic Field and Current
Consider the magnetic field
\[
\vec{B}(s,\phi,z)=
\begin{cases}
0&0\le s<a\\
\alpha \frac{1}{s}(s^4-a^4)\, \hat{\phi}&a<s<b\\
0&s>b
\end{cases}
\]
- Use step and/or delta functions to write this magnetic field as a single expression valid everywhere in space.
- Find a formula for the current density that creates this magnetic field.
- Interpret your formula for the current density, i.e. explain briefly in words where the current is.
- Path Independence
The gravitational field due to a spherical shell of mass is given by: \begin{equation} \vec g =\begin{cases} 0&r<a\\ -\frac{4}{3}\pi\rho\,G\left({r}-\frac{a^3}{r^2}\right)\hat{r}&a<r<b\\ -\frac{4}{3}\pi\rho\, G\left(\frac{b^3-a^3}{r^2}\right)\hat{r}&b<r\\ \end{cases} \end{equation} where \(a\) is the inside radius of the shell, \(b\) is the outside radius of the shell, and \(\rho\) is the constant mass density.
-
Using an explicit line integral, calculate the work required to
bring a test mass, of mass \(m_0\), from infinity to a point \(P\),
which is a distance \(c\) (where \(c>b\)) from the center of the shell.
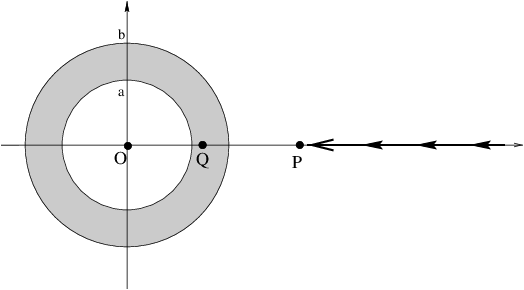
- Using an explicit line integral, calculate the work required to bring the test mass along the same path, from infinity to the point \(Q\) a distance \(d\) (where \(a<d<b\)) from the center of the shell.
- Using an explicit line integral, calculate the work required to bring the test mass along the same radial path from infinity all the way to the center of the shell.
-
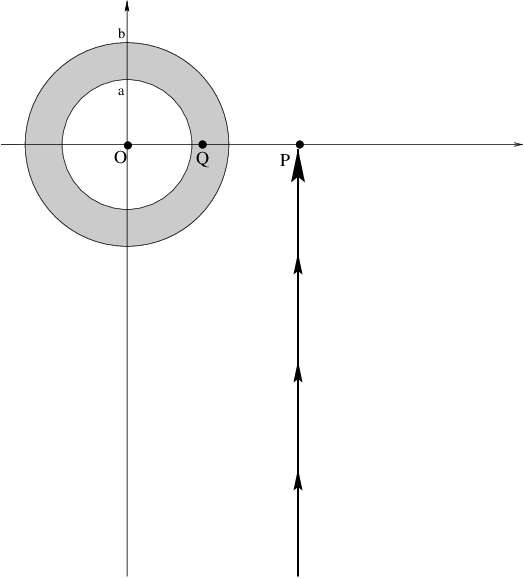
Using an explicit line integral, calculate the work required to
bring in the test mass along the path drawn below, to the point \(P\)
of the first question. Compare the work to your answer from the first question.
-
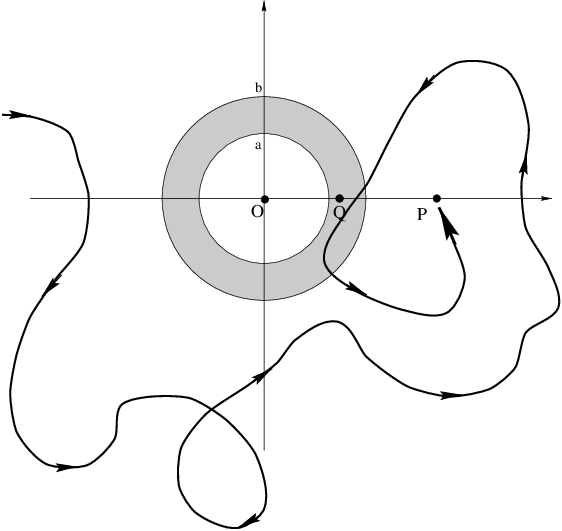
What is the work required to bring the test mass from infinity along
the path drawn below to the point \(P\) of question a. Explain your
reasoning.
-
Using an explicit line integral, calculate the work required to
bring a test mass, of mass \(m_0\), from infinity to a point \(P\),
which is a distance \(c\) (where \(c>b\)) from the center of the shell.