Fourier Coefficients of a Cuspy-looking Function

• Oscillations and Waves 2023

  This problem gives practice with evaluation of the \(a_0\) term. It is written as a single function, but to do the integral by hand is to deal with the \(t>0\) and \(t<0\) parts separately. Also, save yourself some work by considering the symmetry of the function ... what can you say about the integrals on the \(t>0\) and \(t<0\) sides?
  

  A periodic function is given over one period \(T\) by \[V(t)=V_0 e^{-\gamma|t|/T};\,\,\,\,(\gamma=30)\text{(and then repeated forever).}\]

  

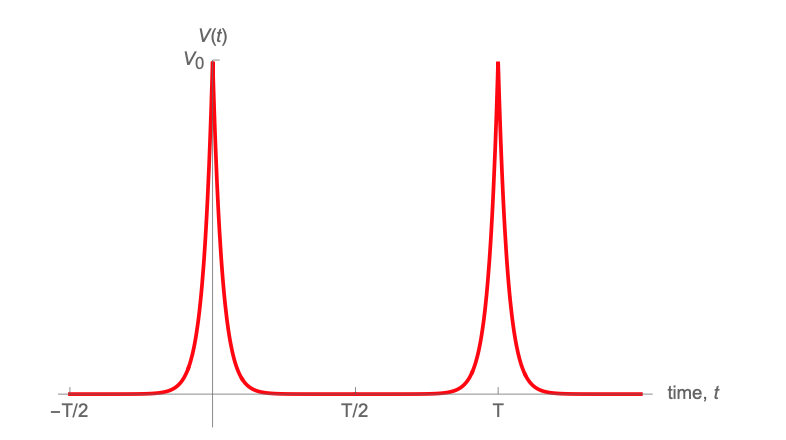
  With this choice of time origin, find the constant term and the next \(2\) coefficients of the Fourier series. Note that the function parameter \(\gamma=30\) has been chosen so that “\(T/2\)” is effectively “at infinity”, so you can change the limits of the integral to infinity to make it easier to evaluate.
  

  You may also use Mathematica (or similar) to evaluate integrals. (You can even use the built-in function to check your answer, but it is not a valid solution to simply say, “Here are the coefficients because Mathematica said that's what they are!") We are learning how to evaluate the coefficients. the point of this question is for you to demonstrate that you understand how to set up and solve the problem and that you can guide a novice reader through the solution.
  

  Comment: this problem is a first step to understanding the “Fourier transform” (which represents a non-repeating function) as distinct from the Fourier series (which represents a periodic or repeating function). If we try to represent a non-repeating function, one step is to let the “period of repetition” go to infinity.